
The final part (the red curve) has also positive slopes but increases in angles so all its velocities are positive and increasing in magnitude as well.Īll these explanations correspond to (d). In fact, the object continues moving just at the same velocity in the last second of the previous part. This indicates that the velocity must be constant in that time interval. The middle part (the red straight line) has a constant slope in its time interval. As you can see, in all this time interval, the slopes have acute angles and are decreasing so the velocities must be negative and decreasing in magnitude for this time interval. In the first part (the blue curve), the slope at the starting point, which shows the initial velocity, has an acute angle so $v_0>0$. Notice that these angles are measured with the positive $x$-axis. Slopes with an acute angle ($\alpha90^\circ$) show a negative velocity. The slope of a tangent line at each point of a $x-t$ curve gives the velocity of the object.

Solution: This motion is composed of three parts, two curves, and one straight line.

Which of the following graph is the corresponding velocity vs.
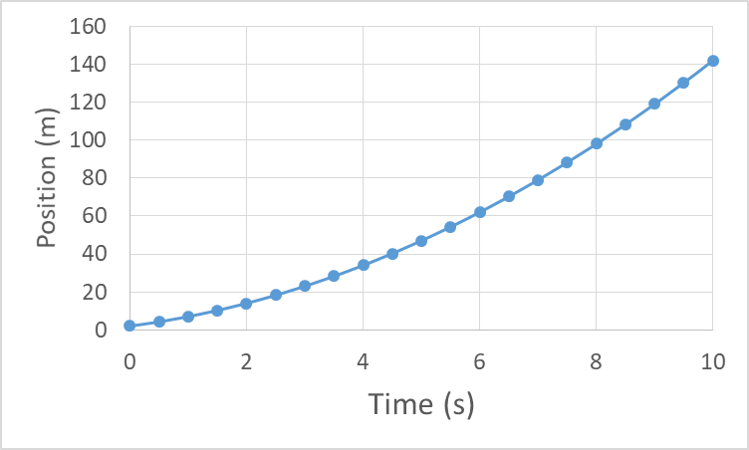
time graph for a moving object along the $x$ axis is shown in the figure below. For each section of kinematics, you can find, here, an answered multiple-choice question. AP Physics 1: Kinematics Practice Problems with AnswersĪ complete set of multiple-choice questions about kinematics in the AP Physics 1 exam are gathered here.


 0 kommentar(er)
0 kommentar(er)
